Wase Solution | DBMS Solved
1. Please read the information given below before attempting the questions that follow. [3+3]
EmpMaster (eid: number, ename: varchar, sal: number, age: number, deptid: number)
Dept(deptid: number, budgetAmt: number, floor: number, mgreid: number)
Salaries range from Rs.10,000 to Rs.100,000, ages vary from 20 to 80, each department has about five employees on average, there are 10 floors, and budgets vary from RS.10,000 to Rs 100,000. You can assume uniform distribution of values.
Query1: Print ename, age, and sal for all employees.
Query2: Find the deptids of departments that are on the 10th floor and have a budget of less than Rs25,000
1.1 For each of the following queries, which index would you choose to speed up the query? [2.5]
1.2 If your database system does not consider index-only plans (i.e.,data records are always retrieved even if enough information is available in the index entry), how would your answer change? [2.5]
Explain your answers briefly.
Answer
We should create an unclustered hash index on ename, age, sal fields of EmpMaster since then we could do on index only scan. If our system does not include index only plans then we should not create index for this query. Since this query requires us to access all the Emp records, an index won’t help us any, and so should we access the records using a filescan.
We should create a clustered dense B+tree index on floor, budget fields of Dept, since the records would be ordered on these fields then. So when executing this query, the first record with floor=10 must be retrieved, and then the other records with floor =10 can be read in order of budget. This plan, which is the best for this query, is not an index-only plan.
2. Consider the following relations: [1×5=5]
Student (snum: integer, sname: string, major: string, level: string, age: integer)
Class (name: string, meets at: string, room: string, fid: integer)
Enrolled (snum: integer, cname: string)
Faculty (fid: integer, fname: string, deptid: integer)
The meaning of these relations is straightforward; for example, Enrolled has one record per student-class pair such that the student is enrolled in the class.
Write the following queries in SQL. No duplicates should be printed in any of the answers.
2.1 Find the age of the oldest student who is either a History major or enrolled in a course taught by ‘I. Teach’.
2.1 Find the names of all classes that either meet in room R128 or have five or more students enrolled.
2.1 Find the names of all students who are enrolled in two classes that meet at the same time.
2.1 Find the names of students enrolled in the maximum number of classes.
2.1 For each age value that appears in Students, find the level value that appears most often. For example, if there are more FR level students aged 18 than SR, JR, or SO students aged 18, you should print the pair (18, FR).
Answers:
- SELECT MAX(S.age) FROM Student S WHERE (S.major = ‘History’) OR S.snum IN (SELECT E.snum FROM Class C, Enrolled E, Faculty F WHERE E.cname = C.name AND C.fid = F.fid AND F.fname = ‘I.Teach’ )
- SELECT C.name FROM Class C WHERE C.room = ‘R128’ OR C.name IN (SELECT E.cname FROM Enrolled E GROUP BY E.cname HAVING COUNT (*) >= 5)
SQL: Queries, Constraints, Triggers 47
- SELECT DISTINCT S.sname FROM Student S WHERE S.snum IN (SELECT E1.snum FROM Enrolled E1, Enrolled E2, Class C1, Class C2 WHERE E1.snum = E2.snum AND E1.cname <> E2.cname AND E1.cname = C1.name AND E2.cname = C2.name AND C1.meets at = C2.meets at)
- SELECT DISTINCT S.sname [2] FROM Student S WHERE S.snum IN (SELECT E.snum FROM Enrolled E GROUP BY E.snum HAVING COUNT (*) >= ALL (SELECT COUNT (*) FROM Enrolled E2 GROUP BY E2.snum ))
- SELECT S.age, S.level FROM Student S GROUP BY S.age, S.level, HAVING S.level IN (SELECT S1.level FROM Student S1 WHERE S1.age = S.age GROUP BY S1.level, S1.age HAVING COUNT (*) >= ALL (SELECT COUNT (*) FROM Student S2 WHERE s1.age = S2.age GROUP BY S2.level, S2.age))
- Construct a B+-tree for the following set of key values: [2+2+1=5]
(2, 3, 5, 7, 11, 17, 19, 23, 29, 31)
Assume that the tree is initially empty and values are added in ascending order.
Construct B+-trees for the cases where the number of pointers that will fit
in one node is as follows:
- Four
- Six
- Eight
Answer:The following will be generated by inserting values into the B+-tree inascending order. A node (other than the root) will never be allowed to have fewerthan n/2! Values/pointers.
1. Four Node
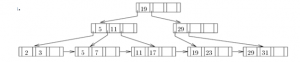
2.Six Node

3.Eight Node

4 Determine whether the following decomposition of SP(S#,Sname,Scity,Status,P#,Pname,Price,qty) is a loss less join decomposition? Write the matrix and show the steps. [5]
Decomposition:
CS(Scity,Status)
SUPP(S#,Sname,Scity)
Part(P3,Pname,Price)
SPN(S#,P#,Qty)
FDs Holding on SP:
S#–>Sname,Scity
ScityàStatus
P#–>Pname,Price
{S#,P#}àQty
Answer:
Ans Since S#–>Scity and ScityàStatus,thus S3àStatus
Therefore, S#àSname,Scity,Status
Make matrix
| S# | Sname | Scity | Status | P# | Pname | Price | qty | |
| CS | b00 | b01 | a2 | a3 | b04 | b05 | b06 | b07 |
| SUPP | a0 | a1 | a2 | b13 | b14 | b15 | b16 | b17 |
| PART | b20 | b21 | b22 | b23 | a4 | a5 | a6 | b17 |
| SPN | a0 | b31 | b32 | b33 | a4 | b35 | b36 | a7 |
Applying FD ScityàStatus,row 0 and 1 match on the value of Scity,So force these two rows to match on the values of Status.Thus replaced b13 in row 1 by a3.
| S# | Sname | Scity | Status | P# | Pname | Price | qty | |
| CS | b00 | b01 | a2 | a3 | b04 | b05 | b06 | b07 |
| SUPP | a0 | a1 | a2 | a3 | b14 | b15 | b16 | b17 |
| PART | b20 | b21 | b22 | b23 | a4 | a5 | a6 | b17 |
| SPN | a0 | b31 | b32 | b33 | a4 | b35 | b36 | a7 |
Now,applying the FD P#–>Pname,Price,row 2 and 3 match on the value of P#,so force these two rows to match on the value of Pname ,Price.Thus replace b35 in row 3 by a5 and replace b36 in row 3 by a6
| S# | Sname | Scity | Status | P# | Pname | Price | qty | |
| CS | b00 | b01 | a2 | a3 | b04 | b05 | b06 | b07 |
| SUPP | a0 | a1 | a2 | a3 | b14 | b15 | b16 | b17 |
| PART | b20 | b21 | b22 | b23 | a4 | a5 | a6 | b17 |
| SPN | a0 | b31 | b32 | b33 | a4 | b35 | a6 | a7 |
Now,applying the FD S#–>Sname,Scity,Status, row 1 and 3 match on the value of S#,so force these two rows to match on the value of Sname,Scity and Status.Thus replace b31 in row 3 by a1:replace b32 in row 3 by a2:replace b33 in row 3 by a3
| S# | Sname | Scity | Status | P# | Pname | Price | qty | |
| CS | b00 | b01 | a2 | a3 | b04 | b05 | b06 | b07 |
| SUPP | a0 | a1 | a2 | a3 | b14 | b15 | b16 | b17 |
| PART | b20 | b21 | b22 | b23 | a4 | a5 | a6 | b17 |
| SPN | a0 | a1 | b2 | a3 | a4 | a5 | a6 | a7 |
The row 3 contains only “a” values:therefore,the above decomposition is a loss less join decomposition of SP.
- Suppose you are given a relation R with four attributes ABCD. For each of the following sets of FDs, assuming those are the only dependencies that hold for R. [10]
(a) Identify the candidate key(s) for R.
(b) Identify the best normal form that R satisfies (1NF, 2NF, 3NF, or BCNF).
(c) If R is not in BCNF, decompose it into a set of BCNF relations that preserve the dependencies.
Perform the above tasks for the following set of functional Dependencies:
5.1. C → D, C → A, B → C
5.2. B → C, D → A
5.3. ABC → D, D → A
5.4. A → B, BC → D, A → C
5.5. AB → C, AB → D, C → A, D → B
Answers:
- (a) Candidate keys: B [2]
(b) R is in 2NF but not 3NF.
(c) C → D and C → A both cause violations of BCNF. One way to obtain a (lossless) join preserving decomposition is to decompose R into AC, BC, and CD.
- (a) Candidate keys: BD [2]
(b) R is in 1NF but not 2NF.
(c) Both B → C and D → A cause BCNF violations. The decomposition: AD, BC, BD (obtained by first decomposing to AD, BCD) is BCNF and lossless and join-preserving.
- (a) Candidate keys: ABC, BCD [2]
(b) R is in 3NF but not BCNF.
(c) ABCD is not in BCNF since D → A and D is not a key. However if we split up R as AD, BCD we cannot preserve the dependency ABC → D. So there is no BCNF decomposition.
- (a) Candidate keys: A [2]
(b) R is in 2NF but not 3NF (because of the FD: BC → D).
(c) BC → D violates BCNF since BC does not contain a key. So we split up R as in: BCD, ABC.
- (a) Candidate keys: AB, BC, CD, AD [2]
(b) R is in 3NF but not BCNF (because of the FD: C → A).
(c) C → A and D → B both cause violations. So decompose into: AC, BCD but this does not preserve AB → C and AB → D, and BCD is still not BCNF because D → B. So we need to decompose further into: AC, BD, CD. However, when we attempt to revive the lost functional dependencies by adding ABC and ABD, we that these relations are not in BCNF form. Therefore, there is no BCNF decomposition.
- Which of the following schedules is (conflict) serializable? Explain with the help of precedence graph. [10]
For each serializable schedule, determine the equivalent serial schedules.
6.1 r1 (X); r3 (X); w1(X); r2(X); w3(X) (2Marks)
6.2 r1 (X); r3 (X); w3(X); w1(X); r2(X) (2Marks)
6.3 r3 (X); r2 (X); w3(X); r1(X); w1(X) (2Marks)
6.4 r3 (X); r2 (X); r1(X); w3(X); w1(X)(2Marks)
Soln [2 marks for each 2 marks for the equivalent serial of (c)]
Let there be three transactions T1, T2, and T3. They are executed concurrently and produce a schedule S. S is serializable if it can be reproduced as at least one serial schedule.
A schedule S is to be conflict serializable if it is (conflict) equivalent to some serial schedule S’. In such a case, we can reorder the nonconflicting operations in S until we form the equivalent serial
schedule S’.(2 Marks)
(a) This schedule is not serializable because T1 reads X (r1(X)) before T3 but T3 reads X
(r3(X)) before T1 writes X (w1(X)), where X is a common data item. The operation
r2(X) of T2 does not affect the schedule at all so its position in the schedule is
irrelevant. In a serial schedule T1, T2, and T3, the operation w1(X) comes after r3(X),
which does not happen in the question..(2 Marks)
(b) This schedule is not serializable because T1 reads X ( r1(X)) before T3 but T3 writes X
(w3(X)) before T1 writes X (w1(X)). The operation r2(X) of T2 does not affect the
schedule at all so its position in the schedule is irrelevant. In a serial schedule T1, T3,
and T2, r3(X) and w3(X) must come after w1(X), which does not happen in the question.
.(2 Marks)
(c) This schedule is serializable because all conflicting operations of T3 happens before
all conflicting operation of T1. T2 has only one operation, which is a read on X (r2(X)),
which does not conflict with any other operation. Thus this serializable schedule is
equivalent to r2(X); r3(X); w3(X); r1(X); w1(X) serial schedule.
.(2+2 Marks)
(d) This is not a serializable schedule because T3 reads X (r3(X)) before T1 reads X (r1(X))
but r1(X) happens before T3 writes X (w3(X)). In a serial schedule T3, T2, and T1, r1(X)
will happen after w3(X), which does not happen in the question..(2 Marks)
7 Consider the below snapshot of concurrent execution for immediate update of recovery. [10]
Assuming Check Points: C1, C2, C3, C4 and Transactions: t1, t2…. t16; what are the outcomes of the following tables at all the above 4 check points? (2.5X 4= 10 Marks)
- Active Table
- Commit Table
Answer:
| C1 | Active Table | Commit Table |
| t5, t8, t12 | t1, t6, t14 |
| C2 | Active Table | Commit Table |
| t2, t11, t15 | t1, t6, t5, t8, t12, t14 |
| C3 | Active Table | Commit Table |
| t4, t10, t9, t13 | t2, t11, t15, t1, t6, t5, t8, t12, t14 |
| C4 | Active Table | Commit Table |
| t7, t16 | t4, t10, t9, t13 ,t2, t11, t15, t1, t6, t5, t8, t12, t14 |